Question
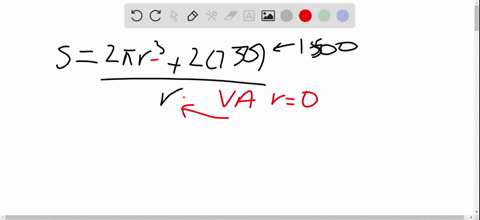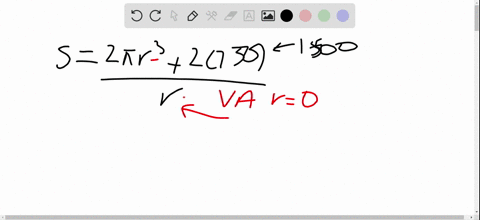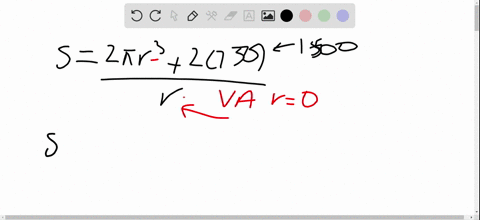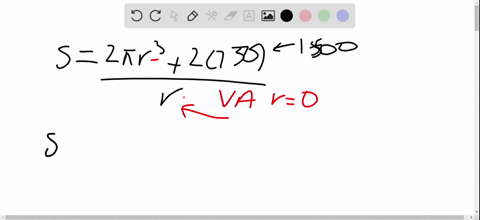
CAS 14. Suppose we are planning to make a taco from a round tortilla with diameter 8 inches by bending the tortilla so that it is shaped as if it is partially wrapped around a circular cylinder. We will fill the tortilla to the edge (but no more) with meat, cheese, and other ingredients. Our problem is to decide how to curve the tortilla in order to maximize the volume of food it can hold. (a) We start by placing a circular cylinder of radius $r$ along a diameter of the tortilla and folding the tortilla around the cylinder. Let $x$ represent the distance from the center of the tortilla to a point $P$ on the diameter (see the figure). Show that the cross-sectional area of the filled taco in the plane through $P$ perpendicular to the axis of the cylinder is $A(x) = r\sqrt{16 - x^2} - \frac{1}{2}r^2 \sin^{-1}(\frac{2}{r}\sqrt{16 - x^2})$ and write an expression for the volume of the filled taco. (b) Determine (approximately) the value of $r$ that maximizes the volume of the taco. (Use a graphical approach with your CAS.)
CAS 14. Suppose we are planning to make a taco from a round tortilla with diameter 8 inches by bending the tortilla so that it is shaped as if it is partially wrapped around a circular cylinder. We will fill the tortilla to the edge (but no more) with meat, cheese, and other ingredients. Our problem is to decide how to curve the tortilla in order to maximize the volume of food it can hold.
(a) We start by placing a circular cylinder of radius $r$ along a diameter of the tortilla and folding the tortilla around the cylinder. Let $x$ represent the distance from the center of the tortilla to a point $P$ on the diameter (see the figure). Show that the cross-sectional area of the filled taco in the plane through $P$ perpendicular to the axis of the cylinder is
$A(x) = r\sqrt{16 - x^2} - \frac{1}{2}r^2 \sin^{-1}(\frac{2}{r}\sqrt{16 - x^2})$
and write an expression for the volume of the filled taco.
(b) Determine (approximately) the value of $r$ that maximizes the volume of the taco. (Use a graphical approach with your CAS.)
Show more…

Added by Joanna D.
Instant Answer
Step 1
### Show more…
Show all steps