Snapsolve any problem by taking a picture.
Try it in the Numerade app?

This problem has been solved

You'll get a detailed solution from a subject matter expert that helps you learn core concepts.

Question

(a) Construct a 3 by 3 system that needs two row exchanges to reach a triangular form and a solution. (b) Construct a 3 by 3 system that needs a row exchange to keep going, but breaks down later.

   (a) Construct a 3 by 3 system that needs two row exchanges to reach a triangular form and a solution.
(b) Construct a 3 by 3 system that needs a row exchange to keep going, but breaks down later.

Linear Algebra and Its Applications

Gilbert Strang 4th Edition

Chapter 1, Problem 14

Instant Answer

Step 1

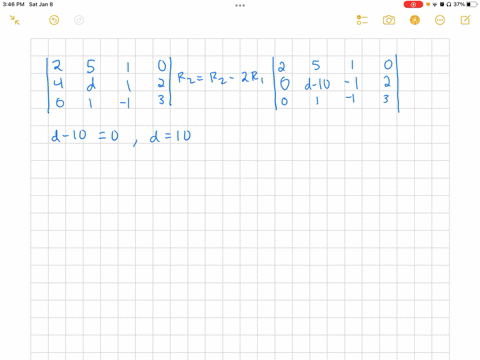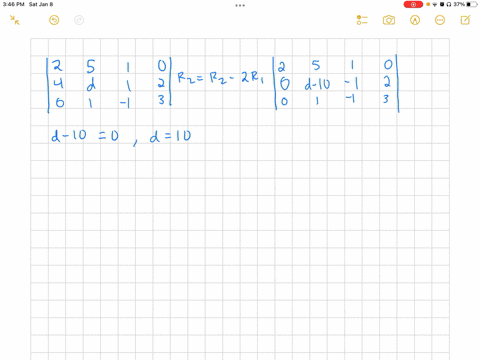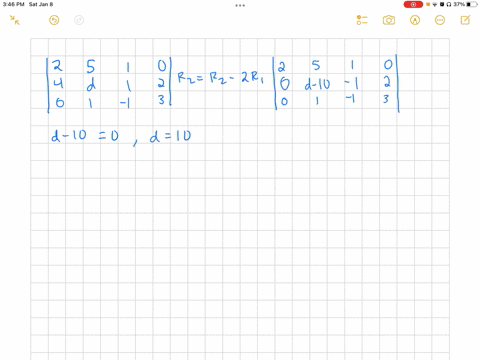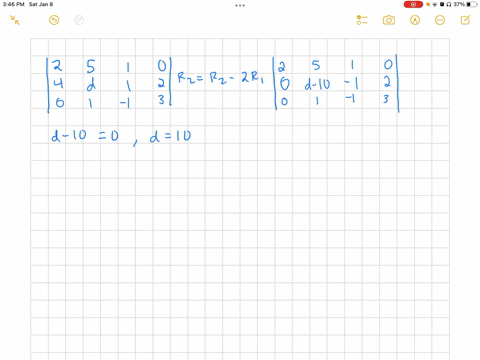
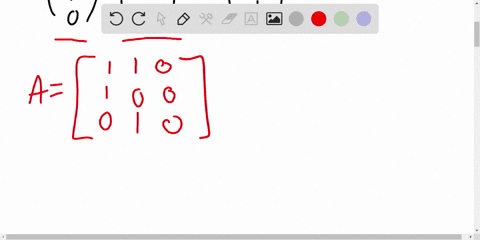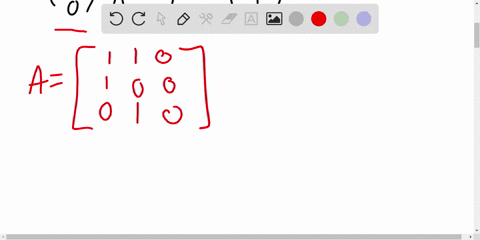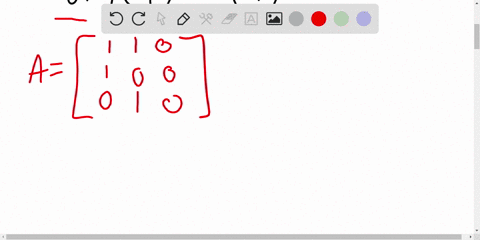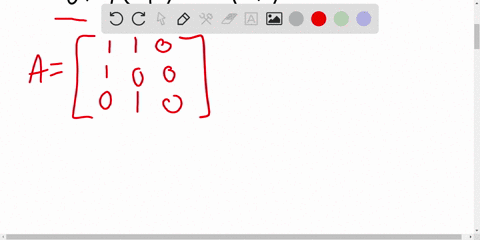
We can start with the following system of equations: \[ \begin{align*} 0x + 0y + z &= 1 \\ x + y + z &= 2 \\ 2x + 3y + 4z &= 3 \end{align*} \] This system needs two row exchanges to reach a triangular form. First, we can swap the first and second rows, and then Show more…

Show all steps

Victor Salazar and 63 other educators are ready to help you.

Ask a new question