00:01
When running goodness of fit tests and tests of independence, they are generally right -to -tailed tests.
00:08
Why? and in order to answer this, i want you to think about the kai square distribution and its shape and its characteristics.
00:18
So its shape is a skewed right graph, and we never have negative kye square values.
00:26
It always starts at zero.
00:27
And as we continue up that x -axis, we're getting into larger and larger, larger values of kai square.
00:37
And when you think about what the goodness of fit test tests, or what the test of independence is actually testing, we are trying to decide whether observed data, the expected data.
01:17
So if it fits, that means it's close.
01:20
It's where you thought it was going to be.
01:23
So i wanted to just take look at two examples.
01:28
So if i gave you this example of observed and expected data, and we observed numbers like 2, 3, 4, and 5, and we expected 2, 2, 3, and 4, you would say that they pretty much fit what was expected.
01:53
And then if we look at this example here of observed and expected, we observed a two, but we expected a five.
02:08
Well, we're not quite there.
02:10
We observed an eight, but we expected only two.
02:14
We observed a three, but we expected ten.
02:18
And we observed a five, and we expected one.
02:21
Well, you can say that this data doesn't fit as well as the previous data.
02:32
This one over here fits better or is closer to what we were expecting than this one over here.
02:40
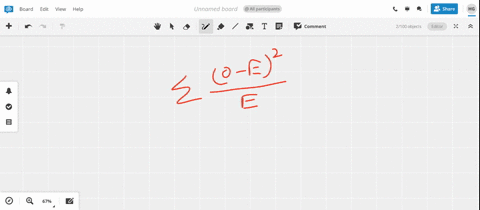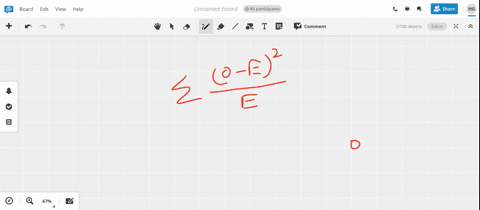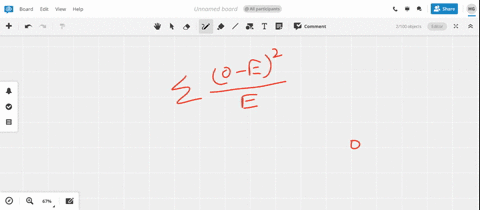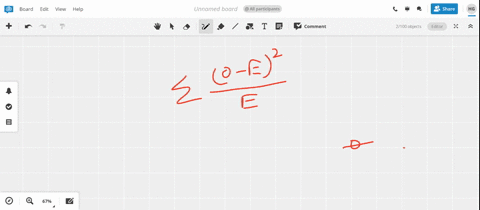
Okay, so now let's also think about how we find our kai square test statistic...




Intro Stats / AP Statistics educators are ready to help you.