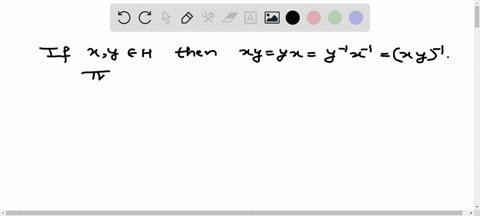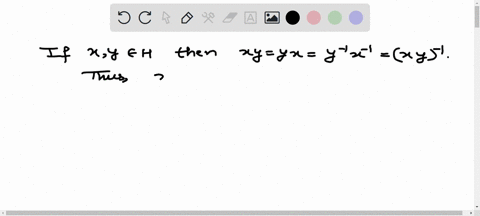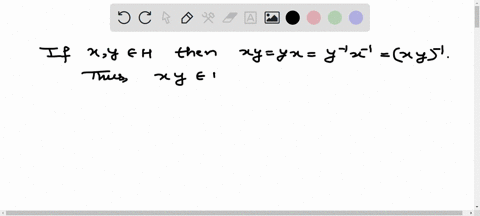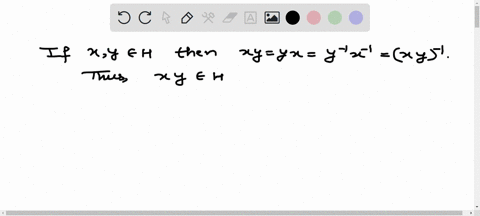
Question
Let $H$ be a subgroup of a finite abelian group $G$. Show that $G$ has a subgroup that is isomorphic to $G / H$.
Let $H$ be a subgroup of a finite abelian group $G$. Show that $G$ has a subgroup that is isomorphic to $G / H$.
Chapter 1, Problem 43

Instant Answer
Step 1
Since $G$ is a finite abelian group, we can write it as a direct sum of cyclic groups: $G \cong \mathbb{Z}_{p_1^{e_1}} \oplus \mathbb{Z}_{p_2^{e_2}} \oplus \cdots \oplus \mathbb{Z}_{p_n^{e_n}}$, where $p_i$ are prime numbers and $e_i$ are positive integers. Show more…
Show all steps