Snapsolve any problem by taking a picture.
Try it in the Numerade app?

This problem has been solved

You'll get a detailed solution from a subject matter expert that helps you learn core concepts.

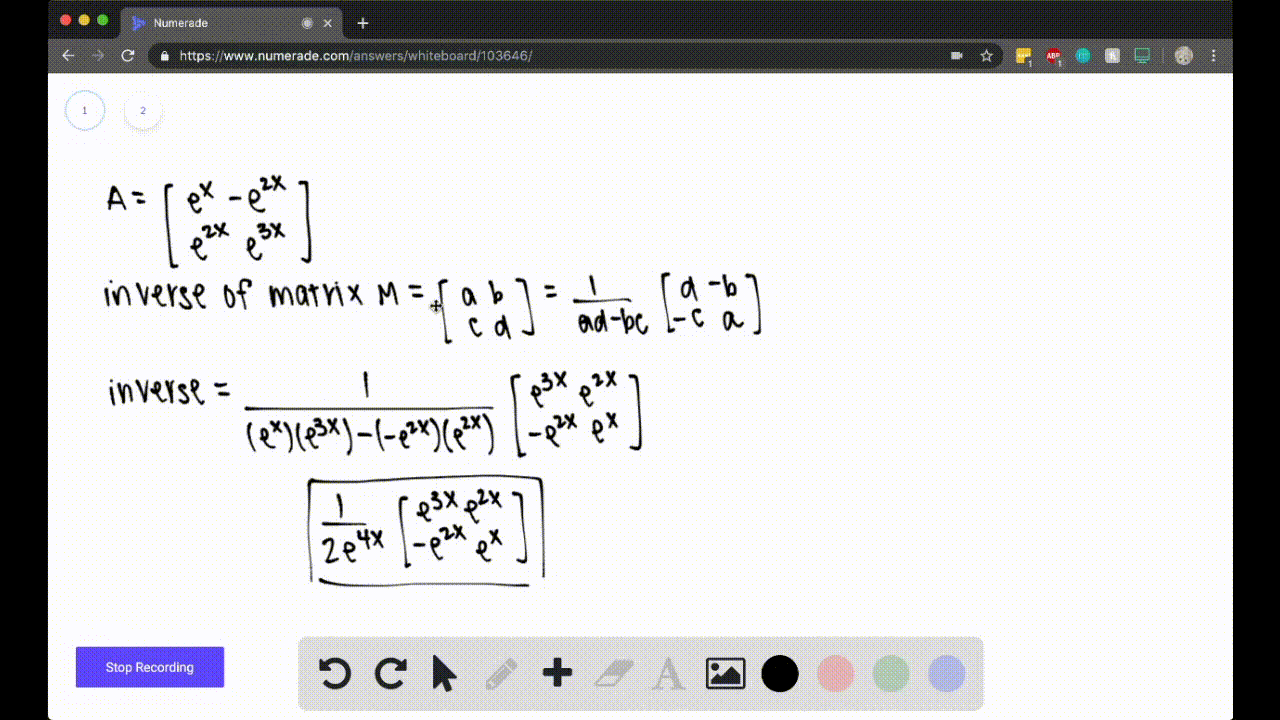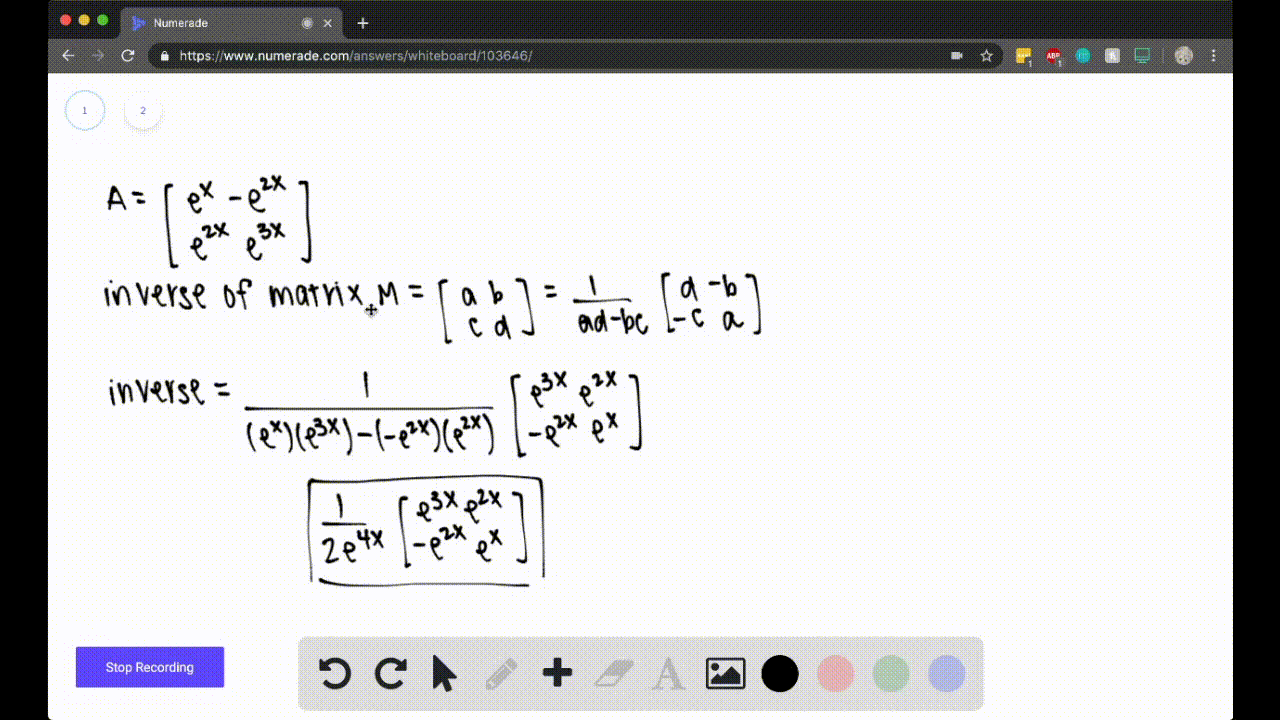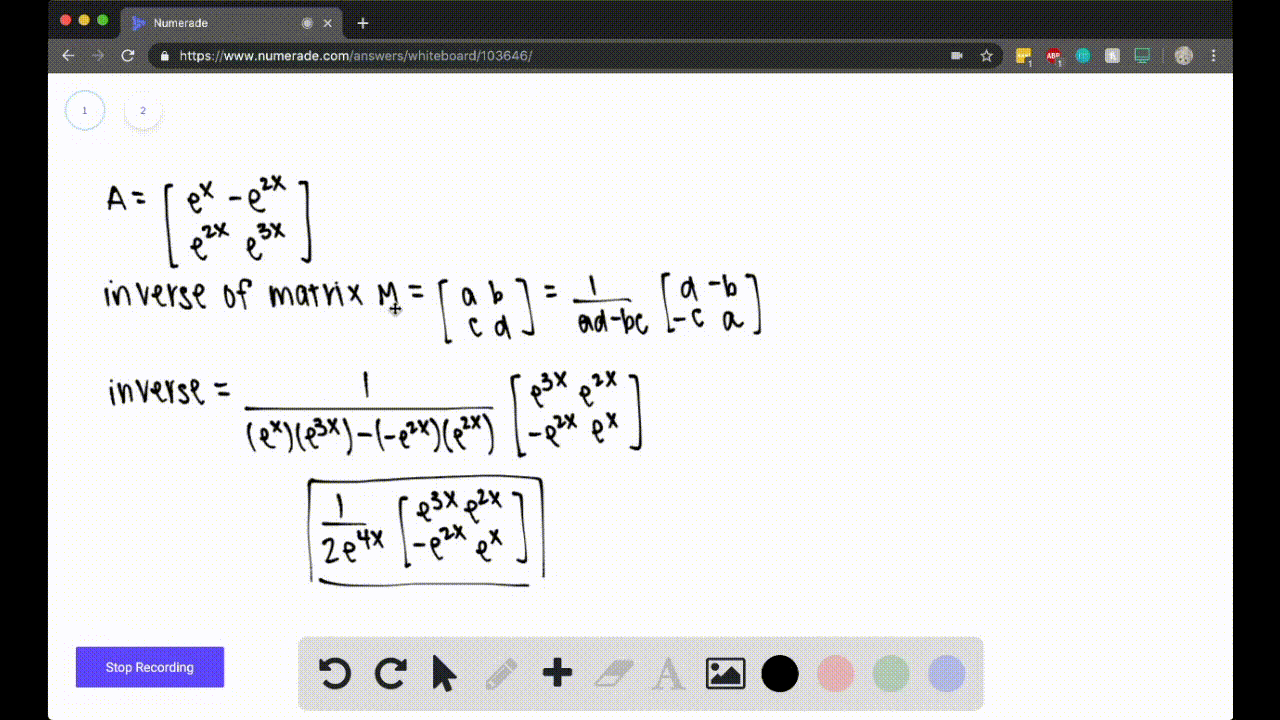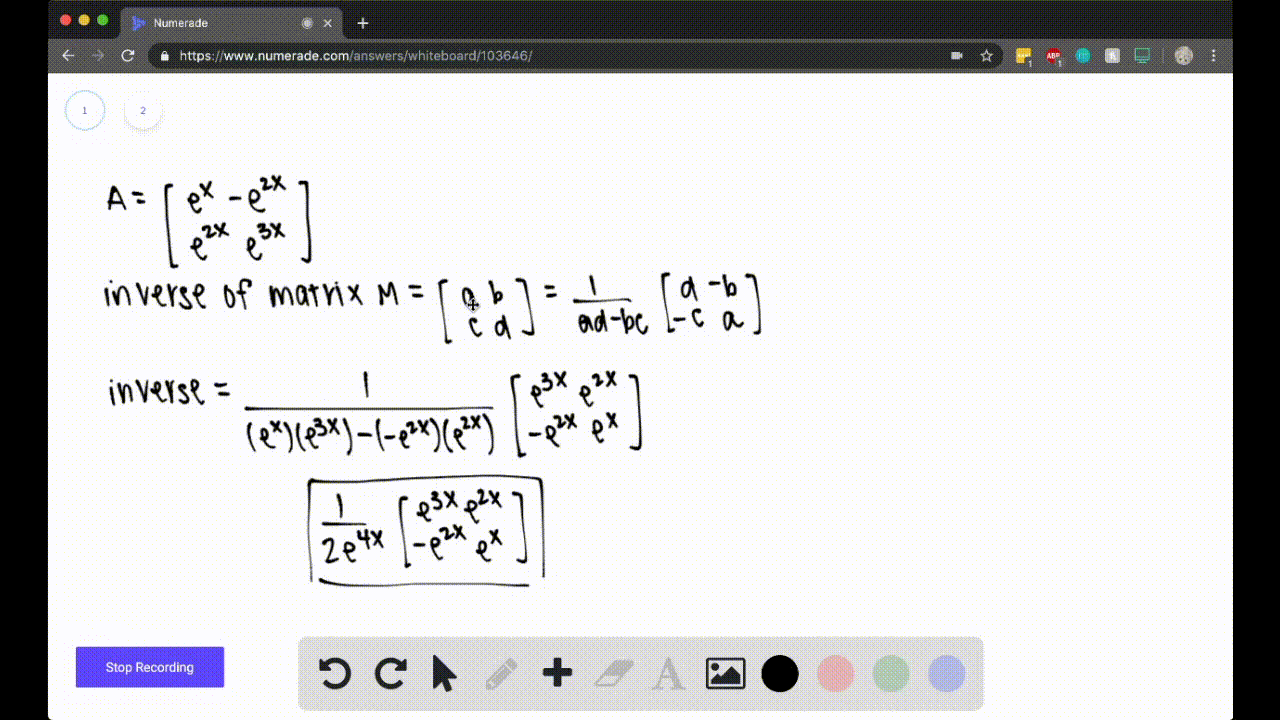
Question

$57-60$ When Do Matrices Have Inverses? Find the inverse of the matrix. For what value(s) of $x,$ if any, does the matrix have no inverse? $$\left[ \begin{array}{rrr}{1} & {e^{x}} & {0} \\ {e^{x}} & {-e^{2 x}} & {0} \\ {0} & {0} & {2}\end{array}\right]$$

   $57-60$ When Do Matrices Have Inverses? Find the inverse of
the matrix. For what value(s) of $x,$ if any, does the matrix have no
inverse?
$$\left[ \begin{array}{rrr}{1} & {e^{x}} & {0} \\ {e^{x}} & {-e^{2 x}} & {0} \\ {0} & {0} & {2}\end{array}\right]$$

Show more…

Algebra and Trigonometry

Algebra and Trigonometry

James Stewart,… 4th Edition

Chapter 11, Problem 59

Instant Answer

Step 1

Step 1: First, we set up our matrix with the identity matrix on the right side: $$\left[ \begin{array}{rrr|rrr}{1} & {e^{x}} & {0} & {1} & {0} & {0} \\ {e^{x}} & {-e^{2 x}} & {0} & {0} & {1} & {0} \\ {0} & {0} & {2} & {0} & {0} & {1}\end{array}\right]$$ Show more…

Show all steps

lock

Taylor Shimono and 67 other subject Algebra educators are ready to help you.

Ask a new question

Recommended Videos

Transcript

00:01 In this problem, we want to find the inverse of our matrix.

00:04 And so we know that in order to do so, we're essentially just going to get rid of this right bracket and replace it with a dashed line.

00:13 And then we're going to write up an identity matrix on the right -hand side.

00:19 And so essentially we're just going to perform row operations on the left -hand side of our matrix in order to row reduce it to the identity matrix.

00:28 And whenever we're left with on the right -hand side of our dash -line is going to.

00:31 To be our inverse matrix.

00:34 So right now our 1 is in the proper position here.

00:38 And we have a 0 in our third row.

00:40 So we can go ahead and divide row 2 by e to the x power.

00:46 And then also in the same step, i'm just going to divide row 3 by 2 in order to get rid of that 2, or 2 changed into a 1.

00:55 So this is going to become a row 1 stays the same.

00:59 So 1, e to the x, 0, 1, 0.

01:03 0 in row 2 and we divide by e to the x we're going to get 1 and we know that we can rewrite negative e to the 2x as negative e squared times e to the x power so if we divide this or e to the x times e to the x power so if we divide this by e to the x we're just going to be left with negative e to the x power and then finally 0.

01:31 And on the right -hand side, we're left with 0, e -to -the -negative x, 0.

01:37 And in our third row, we said that we just divided by 2...

Previous Question